PINN - Physics-Informed Neural Network

Inverse Modeling Neural Network with Physics-Informed Loss

This approach combines data-driven learning with physics-based modeling to infer key physical parameters from observed data. The goal is to develop a neural network–physics hybrid model that enables inverse modeling of dynamic systems, using simulation constraints to ensure physically meaningful predictions. This framework is especially relevant for applications such as reduced-order modeling (ROM) in biomedical systems, e.g., predicting the progression of arterial occlusion from noninvasive measurements like tissue oxygenation.

Purpose

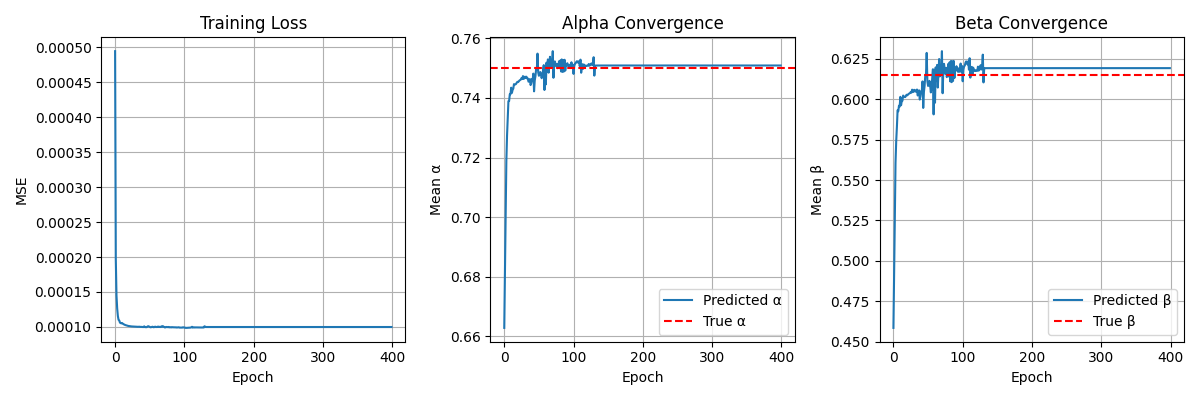
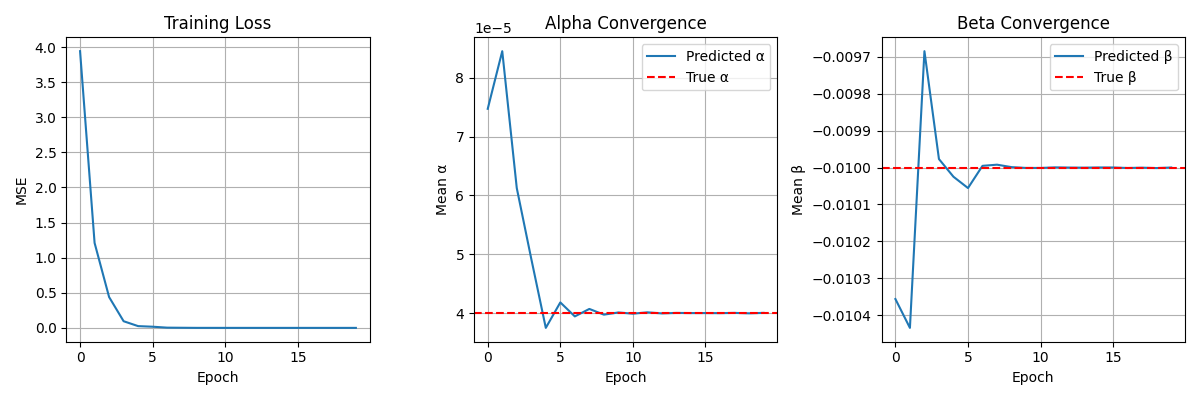
The primary objective is to infer hidden physical parameters—such as diffusivity and source strength in a heat conduction model—by comparing simulated outputs driven by learned parameters to noisy observed data. Unlike traditional forward models, which predict system behavior from known parameters, inverse modeling solves the harder problem of recovering the parameters themselves.

Advantages

End-to-End Differentiability: The entire model, including the physics solver, is differentiable, enabling gradient-based training.
Physical Interpretability: The learned features correspond to meaningful physical quantities.
Simulation-Consistent Learning: The model respects the underlying physics throughout the learning process.
Efficiency: The model learns a reduced representation of a full simulation, offering potential speed-ups during deployment.

Feasibility and Precedents

This methodology is well-supported by existing literature in scientific machine learning. Similar hybrid and physics-informed frameworks have been applied successfully in fields like aerospace, fluid mechanics, and structural dynamics (e.g., Journal of Fluids and Structures, 2017; ERCOFTAC workshops, 2025). These precedents validate both the theoretical soundness and practical relevance of embedding physical constraints into learning pipelines, especially when data are limited and interpretability is critical.

Case 1 — Inverse modeling a 1D heat conduction system with fixed parameters

Code implementation 1

Heat Equation: $ \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2} + \beta \sin(\pi x) $
Analytical Solution: \[ u(x, t) = \sin(\pi x) \left[ e^{-\pi^2 \alpha t} + \frac{\beta}{\pi^2 \alpha}(1 - e^{-\pi^2 \alpha t}) \right] \]
Numerical Solver: Crank–Nicolson scheme is used for time-stepping the PDE numerically in a differentiable manner.
Neural Network: Maps noisy field $u(x, t)$ to $(\alpha, \beta) \in (0, 1)^2$ using a two-layer MLP.
Loss: $\mathcal{L} = \| u_{\text{pred}} - u_{\text{true}} \|^2$, ensuring that learned parameters replicate the observed dynamics.

Case 2 — Inverse modeling a 1D advection–diffusion system with fixed parameters

Code implementation 2

Advection–Diffusion Equation: $ \frac{\partial u}{\partial t} + v \frac{\partial u}{\partial x} = \alpha \frac{\partial^2 u}{\partial x^2} $
Analytical Solution: \[ u(x,t) = \frac{1}{\sqrt{4\pi \alpha t}} \exp\left(-\frac{(x - vt - 0.5)^2}{4\alpha t}\right) \]
Numerical Solver: Implicit finite difference scheme handling both advection and diffusion; inlet conditions are defined by the analytical solution.
Neural Network: Learns to predict $(\alpha, v) \in (0,1)^2$ from noisy snapshots of $u(x,t)$.
Loss: $\mathcal{L} = \| u_{\text{pred}} - u_{\text{true}} \|^2$, ensuring physics-consistent parameter recovery.

Advection-Diffusion training convergence plot

Case 3 — Inverse modeling a 1D advection–diffusion–reaction system with fixed parameters

Code implementation 3

Advection–Diffusion–Reaction Equation: $ \frac{\partial u}{\partial t} + v \frac{\partial u}{\partial x} = \alpha \frac{\partial^2 u}{\partial x^2} + R(u) $, where $ R(u) $ models spatially heterogeneous reaction terms.
Synthesized Data Samples: Noisy measurements of $ u(x,t) $ are generated by simulating the forward PDE solver with known parameters $(\alpha, v, r_0, r_1)$ at random time points. Gaussian noise is added to simulate observation uncertainty.
Numerical Solver: Implicit finite difference scheme that handles all three processes—advection, diffusion, and spatially varying reactions—implemented as a differentiable module for backpropagation.
Neural Network: Maps input pairs of noisy solution fields and time into predicted parameters $(\alpha, v, r_0, r_1)$, using a two-layer MLP with bounded sigmoid output scaled to physical ranges.
Loss: $\mathcal{L} = \| u_{\text{pred}} - u_{\text{true}} \|^2$, comparing simulated outputs under predicted parameters to noisy observations, enabling inverse inference.

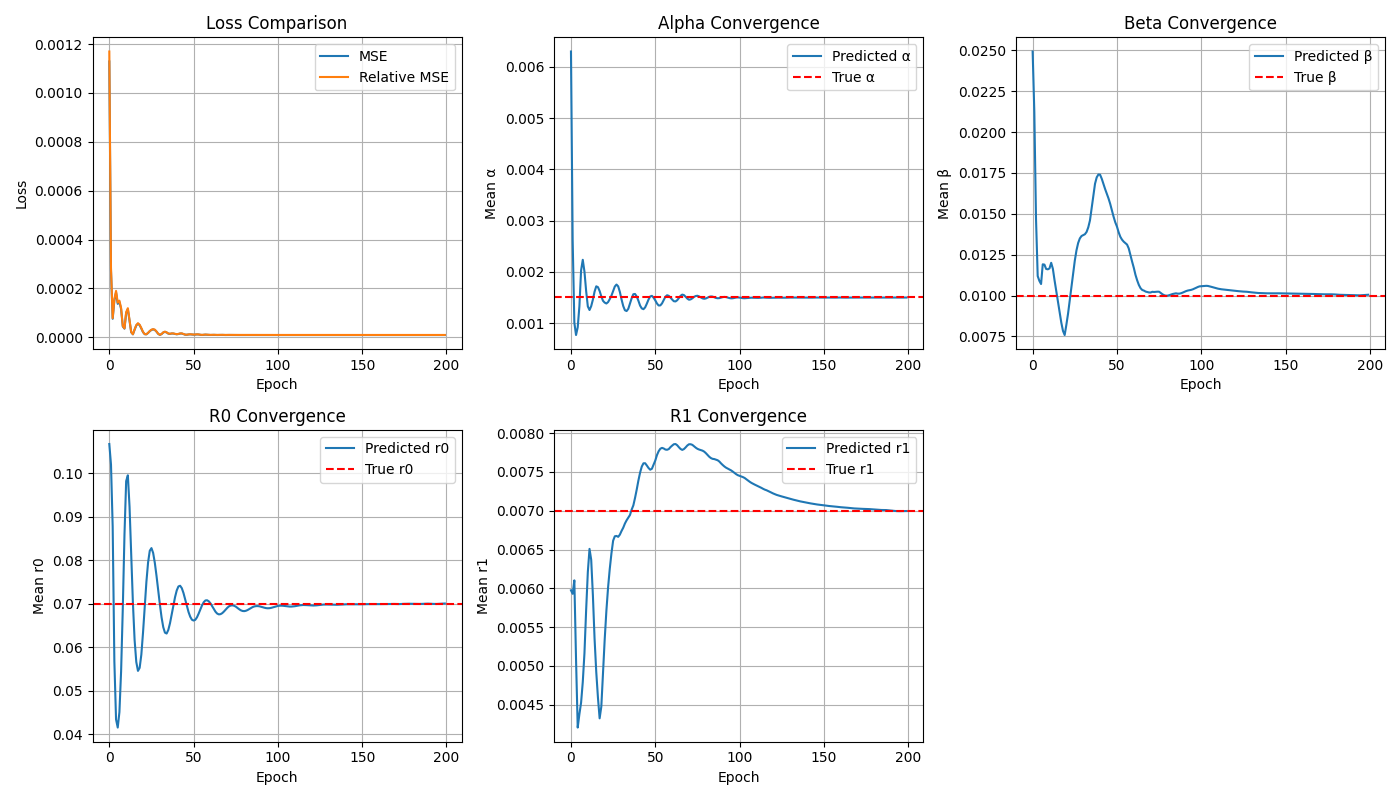
Advection-Diffusion-Reaction training convergence plot

Case 4 — Inverse modeling a 1D hemodynamic system

The governing equations are based on conservation of mass and momentum, expressed in terms of flow rate Q(x,t) and cross‑sectional area A(x,t):

Conservation of Mass:

$$\frac{\partial A}{\partial t} + \frac{\partial Q}{\partial x} = 0$$

Conservation of Momentum:

$$ \frac{\partial Q}{\partial t} + \frac{\partial}{\partial x}\left(\alpha \frac{Q^2}{A}\right) + \frac{A}{\rho}\,\frac{\partial P}{\partial x} = -\,K_R \frac{Q}{A} + \nu\,\frac{\partial^2 Q}{\partial x^2} $$

The pressure $P$ is still given by:

$$ P = P_0 + \beta\left(\sqrt{A} - \sqrt{A_0}\right) $$

To numerically solve these PDEs, boundary conditions are required:

Inlet Boundary Conditions

Prescribe both Q(t) and P(t) (or equivalently A(t)) at the inlet to uniquely define inflow and pressure dynamics.

Outlet Boundary Conditions

Only P(t) is prescribed; Q(t) is inferred using one of four common models:

Dirichlet (Prescribed Pressure): directly specify P(t).
Resistance: P(t) = R Q(t).
RCR (Windkessel): three-element model relating P and Q via resistance and compliance.
Impedance/Structured Tree: uses impedance or structured tree model—Q(t) is computed via convolution with the inverse FT of admittance.

In all cases, the user prescribes P(t) (or its defining parameters), and the solver infers Q(t) based on the chosen outlet model.

Numerical Algorithm

Unknown fields: $P_{i,j}, Q_{i,j}, A_{i,j}$ over $i=0,\dots,N_x-1$; $j=0,\dots,N_t-1$. Total unknowns: 3·N_x·N_t.

Constraints:

Initialization ($j=0$): $P_{i,0}, Q_{i,0}, A_{i,0}$ are prescribed.
Periodicity ($j=N_t-1$): $P_{i,N_t-1}=P_{i,0}$, $Q_{i,N_t-1}=Q_{i,0}$, $A_{i,N_t-1}=A_{i,0}$.
Boundary Conditions:
- Inlet ($i=0$): both $Q_{0,j}$ and $P_{0,j}$ provided.
- Outlet ($i=N_x-1$): $P_{N_x-1,j}$ prescribed; $Q_{N_x-1,j}$ inferred using SimVascular models (Resistance, RCR/Windkessel, Impedance/Structured-tree).
PDE equations (interior nodes $0Mass: \(\frac{A_{j+1,i}-A_{j,i}}{\Delta t} + \frac{Q_{j,i+1}-Q_{j,i-1}}{2\Delta x} = 0$

Momentum: $\frac{Q_{j+1,i}-Q_{j,i}}{\Delta t} + \frac{\partial}{\partial x}(\alpha \frac{Q^2}{A}) + \frac{A}{\rho}\frac{\partial P}{\partial x} + K_R \frac{Q}{A} = 0$

Constitutive: $P_{j,i} - [P_0 + \beta (\sqrt{A_{j,i}} - \sqrt{A_0})] = 0$

Altogether, these give $3(N_t-2)(N_x-2)$ equations matching the interior unknowns.

Solver outline:

Assemble residual vector $\mathbf{R}(U)$ across all unknowns $U = \mathrm{vec}(P,Q,A)$.
Solve nonlinear system $\mathbf{R}(U)=0$ using Newton–Krylov:
- Approximate Jacobian–vector product via finite differences.
- Solve correction $\Delta U$ using GMRES + ILU preconditioner (avoiding direct factorization errors).
Iterate until convergence $\|\mathbf{R}\| < tol$.

This fully couples the 1D system in space and time, enforcing periodic behavior and solving for the complete space-time field in a single unified step.